直列-並列変換

共振回路の解析をする際、直列-並列変換を利用すると、回路が簡略化され解析しやすくなります。

直列-並列変換

直列 → 並列変換: 図1(a)→(b)

図1(a)のアドミタンスをYとすると

\begin{align} Y=\frac{1}{R_s+jX_s}=\frac{R_s}{R_s^2+X_s^2}-j\frac{X_s}{R_s^2+X_s^2} =\frac{1}{R_s\left(1+\frac{X_s^2}{R_S^2}\right)}+\frac{1}{jX_s\left(1+\frac{R_s^2}{X_s^2}\right)} \end{align}

と式変形できます。Q=Xs/Rsとおくと

\begin{align} Y=\frac{1}{R_s(1+Q^2)}+\frac{1}{jX_s(1+Q^{-2})} \end{align}

となります。この式は、Yは抵抗Rs(1+Q²)とリアクタンスjXs(1+Q⁻²)の並列接続であることを意味しています。よって、図1(a)は(b)のように等価変換できます。

直列→並列変換

\begin{align} &Q=\frac{X_s}{R_s}\\ &R_p=R_s(1+Q^2)\\ &X_p=(1+Q^{-2})X_s=\frac{R_p}{Q} \end{align}

変換後のQをQpとして求めてみると

\begin{align} Q_p=\frac{R_p}{X_p}=\frac{R_s(1+Q^2)}{X_s(1+Q^{-2})}=\frac{R_s}{X_s}Q^2=Q \end{align}

となります。直列-並列変換によってQが変化しないことがわかります。

Q≫1の場合はリアクタンス成分はほとんど変化しません。

\begin{align} R_p&=(1+Q^2)R_s\approx Q^2R_s\\ X_p&=(1+Q^{-2})X_s\approx X_s \end{align}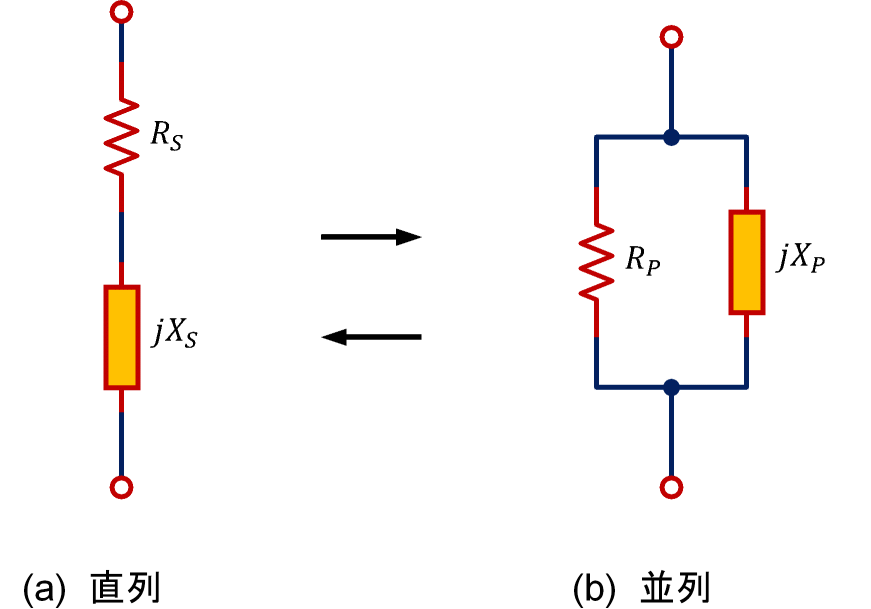

並列 → 直列変換: 図1(b)→(a)

並列→直列変換

\begin{align} &Q=\frac{R_p}{X_p}\\ &R_s=\frac{R_p}{(1+Q^2)}\\ &X_s=\frac{X_p}{1+Q^{-2}}=R_sQ\\ \end{align}

Q≫1の場合はリアクタンス成分はほとんど変化しません。

\begin{align} R_s&=\frac{R_p}{1+Q^2}\approx \frac{R_p}{Q^2}\\ X_s&=\frac{X_p}{1+Q^{-2}}\approx X_p \end{align}

直列-並列変換