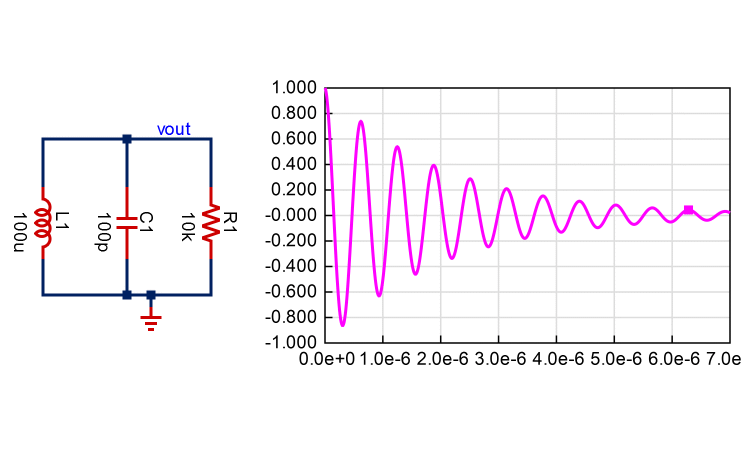
LCタンクのエネルギー散逸(さんいつ)とQの意味

LCタンクの微分方程式

図1のLCタンクの微分方程式:

\begin{align} &\frac{d^2v}{dt^2}+\frac{\omega_0}{Q}\frac{dv}{dt}+\omega_0^2=0\\ &\omega_0=\frac{1}{\sqrt{LC}}\ ,\ Q=\omega_0 CR=\frac{R}{\omega_0 L} \end{align}

を初期条件: v(0)=v0, dv/dt=0として解くと、

LCタンクの電圧

\begin{align} v(t)=\frac{v_0e^{-\frac{\omega_0}{2Q}t}}{\sqrt{1-\frac{1}{4Q^2}}}\sin\left(\sqrt{1-\frac{1}{4Q^2}}\omega_0t+\theta_0\right)\ ,\theta_0=\tan^{-1}\left(2Q\sqrt{1-\frac{1}{4Q^2}}\right) \end{align}

が得られます。Q>>1とすると

\begin{align} v(t)\approx v_0e^{-\frac{\omega_0}{2Q}t}\sin\left(\omega_0t+\frac{\pi}{2}\right) =v_0e^{-\frac{\omega_0}{2Q}t}\cos\omega_0t \end{align}

となります。v(t)は角周波数ω0で振動しながら包絡線が指数関数で減衰することが分かります。

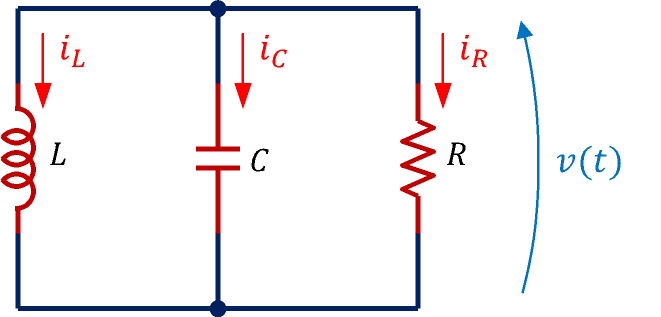
エネルギーの観点から包絡線の式を求めると

Q>>1の場合の包絡線の式はL,Cに蓄えられているエネルギーを利用して求めることができます。「v(t)の波形は局所的に見ると一定振幅で振動し、長い時間スパンで見ると抵抗によるエネルギー消費により徐々に減衰する」と考えます。

\begin{align} v(t)=V(t)\cos\omega_0t \end{align}

と仮定すると、キャパシタに蓄えられているエネルギーEcは

\begin{align} E_C = \frac{1}{2}Cv^2(t) =\frac{1}{2}CV^2(t)\cos^2\omega_0t \end{align}

インダクタに蓄えられているエネルギーE_Lは、i_L≈−i_Cとして

\begin{align} E_L=\frac{1}{2}Li_L^2\approx \frac{1}{2}Li_C^2 = \frac{1}{2}LC^2\left(\frac{dv}{dt}\right)^2 =\frac{1}{2}CV^2(t)\sin^2\omega_0 t \end{align}

となります。両者の和E(t)は

\begin{align} E(t)=E_C+E_L = \frac{1}{2}CV^2(t)(\cos^2\omega_0 t+\sin^2\omega_0 t) =\frac{1}{2}CV^2(t) \end{align}

となります。一方、抵抗Rで消費されるエネルギーは単位時間当たり

\begin{align} P_R = \frac{1}{2}\frac{V^2(t)}{R}=\frac{E(t)}{CR} =\frac{\omega_0}{Q}E(t) \end{align}

となります。エネルギー保存則:

\begin{align} &\frac{dE}{dt}+P_R = 0\\ \rightleftharpoons\ &\frac{dE}{dt}+\frac{\omega_0}{Q}E = 0 \end{align}

を解くと

\begin{align} \text{LCタンク蓄積エネルギー:}\quad &E(t) = E_0e^{-\frac{\omega_0t}{Q}}\\ \text{包絡線:}\quad &V(t)=\sqrt{\frac{2E(t)}{C}} =v_0 e^{-\frac{\omega_0t}{2Q}} \end{align}

が得られます。

Qの意味

上のエネルギー保存則及び包絡線の式でθ=ω₀tとおいて、位相θに関する式として表現すると

\begin{align} \label{eq:lctank_10} \text{エネルギー保存則:}\quad &\frac{dE}{d\theta}+\frac{1}{Q}E=0\ ,\ \theta=\omega_0 t\\ \text{LCタンク蓄積エネルギー:}\quad &E(\theta)=E_0e^{-\frac{\theta}{Q}}\\ \text{包絡線:}\quad &V(\theta)=v_0e^{-\frac{\theta}{2Q}} \end{align}

となります。(\ref{eq:lctank_10})式より

\begin{align} Q=\frac{E}{-\frac{dE}{d\theta}}=\frac{\text{LCタンク蓄積エネルギー}}{\text{位相差1 rad}あたりに消費されるエネルギー} \end{align}

が得られます。これがQの意味です。

θ=2πQ (rad) = Qサイクルで、LCタンクに蓄積されたエネルギーがexp(−2π)=0.2%, 包絡線の振幅がexp(−π)=4%になります。
たとえばQ=100, 100MHzのLCタンクは、100サイクル=1usで振幅が4%になります。