Sパラメータとはなにか
はじめに
数百MHz以上の高周波回路の設計は、Sパラメータを使用するのが標準的な方法となっています。Sパラメータは、二端子対回路理論及び分布定数回路の理解が前提条件であること、視覚化してイメージしにくく、また計算式がやや複雑なため手計算や電卓ではなく専用のソフトウエアの使用が前提であることが、Sパラメータに対する初学者の敷居を高くしています。
Yパラメータ、Zパラメータ、Sパラメータを簡単に説明すると以下のようになります。
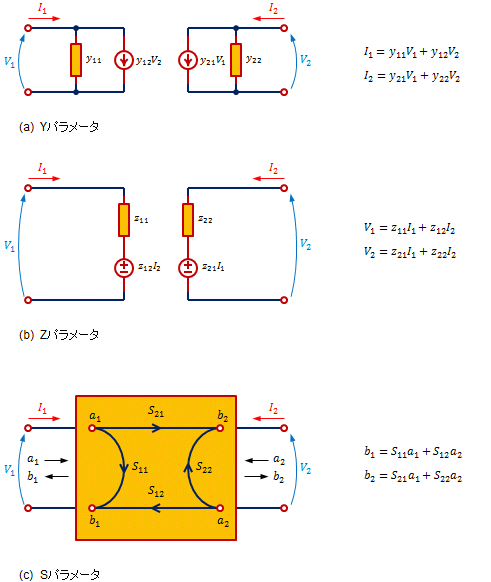
Yパラメータ: 図1(a)
二端子対回路の電流-電圧特性を入力アドミタンスと電流源で表現したもの。各パラメータを求めるには、端子をショート(短絡)して入力アドミタンス、伝達関数を測定します。
Zパラメータ: 図1(b)
二端子対回路の電流-電圧特性を入力インピーダンスと電圧源で表現したもの。各パラメータを求めるには、端子をオープン(開放)にして入力インピーダンス、伝達関数を測定します。
Sパラメータ: 図1(c)
二端子対回路の電圧・電流をそれぞれ入射波成分と反射波成分a1,b1,a2,b2に分解し、電流-電圧特性を入射波、反射波、透過波の間の関係として表現したもの。各パラメータを求めるには、端子を特性インピーダンス(50Ω)で終端して入力インピーダンス、伝達関数を測定します。
高周波回路では、配線の寄生インダクタ成分及び端子の寄生容量成分が無視できず、理想的なショートやオープンが実現できないため、Y,Zパラメータを正確に測定することが困難です。また、トランジスタ回路の場合、ショート・オープンによって回路が発振あるいはトランジスタが破壊される可能性があります。このような理由により、高周波回路ではSパラメータが使用されます。
以降は、Sパラメータについてもう少し掘り下げて解説しています。
電圧・電流を入射波成分と反射波成分で表すと

分布定数回路の理論より、ある位置の電圧・電流は、入射波成分と反射波成分の和として表されます。たとえば、図2の二端子対回路の入力端子のV1,I1を入射波成分と反射波成分で表現すると次式のようになります。
端子電圧・電流と入射波・反射波の関係
V1iは端子電圧V1の入射波成分、V1rは反射波成分です。電流I1の入射波成分及び反射波成分は、電圧V1の入射波成分V1i及び反射波成分V1rと比例関係が成立します(電流の入射波成分=V1i/Z0, 電流の反射波成分=V1r/Z0)。電流の反射波成分は、入射波成分と向きが逆なのでマイナス符号が付きます。
Z0は特性インピーダンスで、伝送線路の材質と形状によって決まります。たとえば、同軸ケーブルの特性インピーダンスは50Ωです。
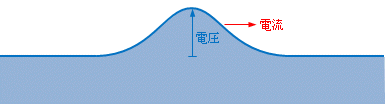
特性インピーダンスの概念は、図3のように電圧=水位、電流=水の流れと考えて、進行する波をイメージすると分かりやすいです。電圧波が進行すると、電圧波と同じ位置に電圧波の進行方向と同じ向きの電流が生じ、それらの比が特性インピーダンスZ0です。
ここで、ひとつ素朴な疑問が生じると思います。一般にプリント基板上に回路を組む際、伝送線路を使用するとは限りません。たとえば図4のように伝送線路を全く使用しない回路の入射波成分・反射波成分・特性インピーダンスの意味はどうなるのか?ということです。
このような場合は、入射波・反射波を無理にイメージせずに、電圧・電流の組(V1,I1)をベクトルと考え、入射波成分・反射波成分をベクトルの成分と考えるのがよいと思われます。次にその根拠を示します。

入射波成分・反射波成分の数学的解釈
上の行列表記の式を数学的視点で見ると、2次元ベクトルを成分に分解する式(1次変換の式)の形をしています。たとえば、ベクトルyが行列Aとベクトルxの積としてy=Axと表されるとすると、
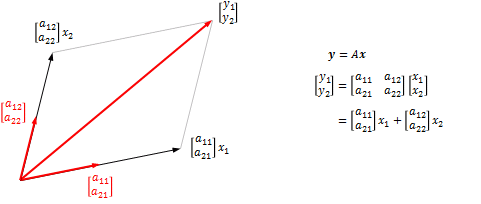
\begin{align} y&=Ax\\ \rightleftharpoons\ \begin{bmatrix}y_1\\y_2\end{bmatrix} &=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} =\begin{bmatrix}a_{11}\\a_{21}\end{bmatrix}x_1 + \begin{bmatrix}a_{21}\\a_{22}\end{bmatrix}x_2 \end{align}より、ベクトルyは$(a_{11},a_{21})$及び$(a_{12},a_{22})$を軸とする成分に分解されることを意味します(図5)。
V1,I1の式についても同様に
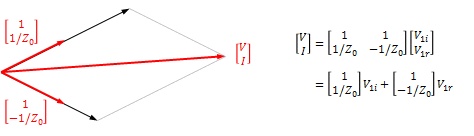
\begin{align} \begin{bmatrix}V_1\\I_1\end{bmatrix} =\begin{bmatrix}1\\\frac{1}{Z_0}\end{bmatrix}V_{1i} +\begin{bmatrix}1\\-\frac{1}{Z_0}\end{bmatrix}V_{1r} \end{align}と表されることから、$V_{1i}$はベクトル$(V_1,I_1)$のベクトル$(1,\frac{1}{Z_0})$上への投影成分、$V_{1r}$はベクトル$(1,-\frac{1}{Z_0})$上への投影成分となります(図6)。
つまり、ある位置の電圧・電流の組$(V_1,I_1)$を2次元ベクトルと考え、特性インピーダンスZ0によって決まる2つのベクトル$(1,\frac{1}{Z_0})$及び$(1,-\frac{1}{Z_0})$を座標軸とする2つの成分に分解したときの各成分が入射波成分$V_{1i}$及び反射波成分$V_{1r}$となります。
一般にベクトルを成分に分解して演算すると、座標軸の選び方によらず結果が一意に決まりますが、回路の電圧・電流を入射波成分・反射波成分に分解して解析する際も、特性インピーダンスZ0の選び方によらず結果が一意に決まります。 図4のように伝送線路を全く使用しない回路において電圧・電流を入射波成分・反射波成分に分解する際、特性インピーダンスZ0は任意に設定することが可能ですが、通常Z0=50Ωとして解析します。
インピーダンスと反射係数の関係
低周波の回路解析では、電圧・電流とオームの法則を使用して回路方程式を立てますが、分布定数回路やSパラメータ解析では、電圧・電流を入射波成分と反射波成分に分解し、これらの成分を使用して回路方程式を組み立てます。ここでは、オームの法則が、入射波・反射波成分を使用して表現するとどのようになるのかを考えます。
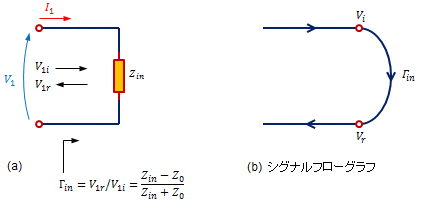
図7(a)の回路において、オームの法則より
\begin{align} \text{オームの法則:}\quad V_1=Z_{in}I_1 \end{align}となります。ここで、V1,I1を特性インピーダンスZ0で入射波成分と反射波成分に分解すると
\begin{align} \begin{cases} V_1 = V_{1i}+V_{ir}\\ I_1 =\frac{1}{Z_0}(V_{1i}-V_{1r}) \end{cases} \end{align}となりますが、これをオームの法則に代入すると次式が得られます。
\begin{align} \text{入射波と反射波の関係:}\quad V_{1r}=\Gamma_{in}V_{1i}\quad ,\ \Gamma_{in}=\frac{Z_{in}-Z_0}{Z_{in}+Z_0} \end{align}上式は、オームの法則を入射波成分と反射波成分を使用して表現した式で、 $\Gamma_{in}$を反射係数といいます。反射係数は入射波と反射波の比でインピーダンスZinと1対1に対応します。
電圧・電流を入射波成分と反射波成分に分解して回路方程式を立てると、オームの法則は、入射波、反射波、反射係数の間の関係式となります。 反射係数とインピーダンスは1対1に対応します。
入射波・反射波の規格化: 正規入射波、正規反射波
Sパラメータの定義では、電圧・電流を入射波成分と反射波成分に分解し、かつ特性インピーダンスの平方根$\sqrt{Z_0}$で規格化した「正規入射波」、「正規反射波」を使用して二端子対回路のふるまいを記述します。
図8のV1を入射波成分と反射波成分に分解すると
\begin{align} V_1=V_{1i}+V_{1r} \end{align}となりますが、V1i, V1rを特性インピーダンスの平方根$\sqrt{Z_0}$で規格化し、
\begin{align} a_1 =\frac{V_{1i}}{\sqrt{Z_0}}\\ b_1 =\frac{V_{1r}}{\sqrt{Z_0}}\\ \end{align}と定義します。a1,b1は「入射波」、「反射波」、「normalized power wave」とよばれますが、このページではV1i,V1rと区別するために「正規入射波」、「正規反射波」とよぶことにします。V1,I1を正規入射波と正規反射波で表現すると次式のようになります。
端子電圧・電流と正規入射波・反射波の関係
また、上式をa1,b1について解くと
正規入射波・反射波と端子電圧・電流の関係
が得られます。上の2式を使用して電圧・電流の組(V1,I1)から正規入射波・正規反射波の組(a1,b1)を、または正規入射波・正規反射波の組(a1,b1)から電圧・電流の組(V1,I1)を求めることができます。(V2,I2)と(a2,b2)の間の関係式も同様です。

Sパラメータの定義
Sパラメータとは、正規入射波a1,a2を独立変数、正規反射波b1,b2を従属変数として二端子対回路を定式化したもので、次式のように定義されます。
Sパラメータの定義
各パラメータは次式より求めることができます。
\begin{align} S_{11} &= \left.\frac{b_1}{a_1}\right|_{a_2=0}=\text{2次側を$Z_0$で終端したときの1次側から見た反射係数}\\ S_{12} &= \left.\frac{b_1}{a_2}\right|_{a_1=0}=\text{1次側を$Z_0$で終端したときの逆方向伝達関数}\\ S_{21} &= \left.\frac{b_2}{a_1}\right|_{a_2=0}=\text{2次側を$Z_0$で終端したときの順方向伝達関数}\\ S_{22} &= \left.\frac{b_2}{a_2}\right|_{a_1=0}=\text{1次側を$Z_0$で終端したときの2次側から見た反射係数}\\ \end{align}※ Sパラメータの測定は、2次側(負荷側)を特性インピーダンスZ0で終端するとa2=0、1次側(信号源側)を特性インピーダンスZ0で終端するとa1=0となることを利用します。
Sパラメータの考え方はYパラメータやZパラメータと同様です。 Yパラメータは端子をショートして求めた入力アドミタンス・伝達関数、Zパラメータは端子をオープンとして求めた入力インピーダンス・伝達関数なのに対し、Sパラメータは端子を特性インピーダンスZ0で終端して求めた反射係数、伝達関数となります。 反射係数はインピーダンス・アドミタンスと1対1に対応する量なので、反射係数=インピーダンス・アドミタンスと考えて問題ありません。