分布定数回路の考え方
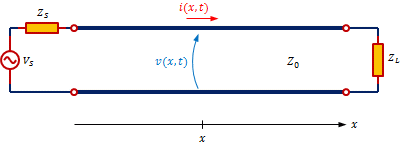
信号線の一端に電圧を印加すると、その電圧は光速に近いスピードで伝搬します。一般に、数100MHz以下の周波数で信号線が短い場合は、入力された信号が瞬時に出力端に到達すると考えて問題ありません。しかし、数GHz以上の高周波信号や装置間を結ぶ同軸ケーブルのように長い距離を伝わる信号については、伝達の遅れが無視できなくなります。このような場合は、信号線を分布定数回路(伝送線路)とみなし、電圧・電流を時間及び位置の関数として取扱います(図1)。
分布定数回路の波動方程式
分布定数回路のふるまいは、図2のように幅Δxの微小区間の中にインダクタとキャパシタが分布している等価回路で解析します。インダクタに電圧が印加されると電流は遅れて増加し、キャパシタに電流が流れると電圧は遅れて増加するので、このモデルによって信号の伝搬遅延が定式化できます。
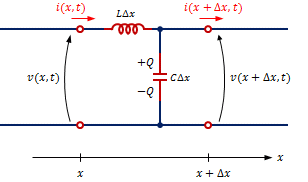
図2の位置xとx+Δxの間の微小要素について回路方程式を立てると
分布定数回路の基礎方程式
が得られます。この2式は波動方程式の素となる方程式で、第1式は「電流の空間的なゆがみによって電圧が時間変化する」、第2式は「電圧の空間的なゆがみによって電流が時間変化する」という意味で、それぞれ音波における連続の式、運動方程式と同じ形をしています。
ある着目する位置の周囲に電流の空間的なゆがみ($\frac{\partial i}{\partial x}$)があると、その位置の電圧が時間変化して($\frac{\partial v}{\partial t}$)電圧の空間的なゆがみが新たにつくられます(第1式)。そして、電圧の空間的なゆがみ($\frac{\partial v}{\partial x}$)によって電流が時間変化して($\frac{\partial i}{\partial t}$)電流の空間的なゆがみが新たにつくられます(第2式)。このように、電圧と電流がお互いに相互作用を及ぼしながら「ゆがみ」が周囲に伝搬、つまり電圧・電流が波動として伝搬します。
上の2式より、vのみに関する式、iのみに関する式が得られます。これを波動方程式といいます。分布定数回路の各位置における電圧・電流は、波動方程式に境界条件を与えて解くことで得られます。
波動方程式
フェーザに関する波動方程式
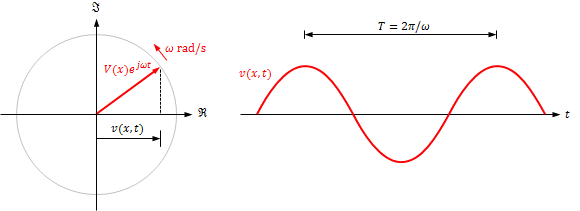
分布定数回路を正弦波で駆動したときの定常状態における電圧・電流は正弦波となるので、
\begin{align} &v(x,t)=\Re[V(x)e^{j\omega t}]\\ &i(x,t)=\Re[I(x)e^{j\omega t}] \end{align}のように複素数を使用して表記します。 $V(x)e^{j\omega t}$は、図3のように複素平面上を正の向き(反時計回り)に角周波数ωで回転するベクトルで、これを実軸へ投影した成分が実際の電圧v(x,t)となります。$I(x)e^{j\omega t}$についても同様です。$V(x)e^{j\omega t}$ と $I(x)e^{j\omega t}$は同じ角周波数で回転しますが、これを時刻t=0で止めたものがV(x), I(x)でそれぞれv(x,t), i(x,t)のフェーザといいます。
複素数で表記したv(x,t), i(x,t)を基礎方程式及び波動方程式に代入すると、フェーザに関する関係式が得られます。
フェーザに関する基礎方程式
フェーザに関する波動方程式
波動方程式の一般解
フェーザに関する波動方程式の一般解は
波動方程式の一般解
となります。C1,C2は複素定数で境界条件によって決まります。
$\boldsymbol{C_1e^{-j\beta x}}$の意味V(x)の式の第1項$C_1e^{-j\beta x}$の意味を考えます。実時間で表記すると
\begin{align} v_i(x,t)=\Re\left[ C_1e^{j(\omega t-\beta x)}\right] \end{align}となります。vi(x,t)は図3と同様に複素平面上を正の向き(反時計回り)に回転するベクトルを実軸へ投影した成分で、時間tに関して正弦波、場所xに関しても正弦波の形状(図4(a))となります。
図4は位置xとx+Δxにおける回転ベクトル$C_1e^{j(\omega t-\beta x)}$, $C_1e^{j(\omega t-\beta (x+\Delta x))}$を図示したものです。これらのベクトルは角周波数ωで回転し、また、位置xの回転ベクトルに対し位置x+Δxの回転ベクトルは位相がβΔxだけ遅れたものとなります。
ここで、図4(b)のように時刻t=0で位置xの回転ベクトルの位相を0とすると、位置x+Δxにおける回転ベクトルの位相は−βΔxとなります。回転ベクトルは角周波数ωで回転しているので、位置x+Δxにおける回転ベクトルは時刻Δt=βΔx/ωに位相が0になります(図4(c))。これは、位相0の点が速度Δx/Δt=ω/βで移動したことを意味します。この速度を位相速度といいます。 よって、$C_1e^{-j\beta x}$は、x軸の正の方向へ伝搬する波を表します。
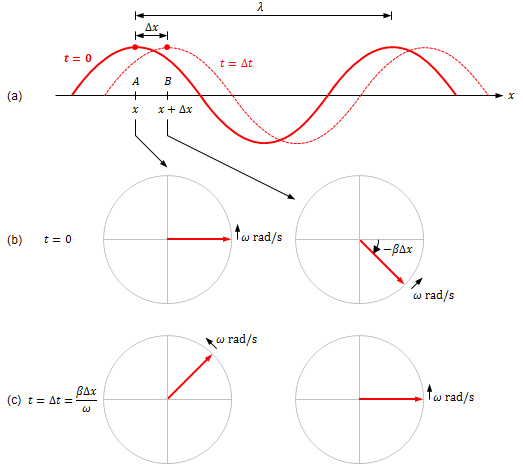
一方、$C_1e^{j\beta x}$はx軸の負の方向へ伝搬する波を表します。波動方程式の解は、「位置xの電圧V(x)は、正の方向へ伝搬する波と負の方向へ伝搬する波の和となる」、「位置xの電流I(x)についても、正の方向へ伝搬する波と負の方向へ伝搬する波の和して表される」ことを意味しています。
特性インピーダンス
波動方程式の一般解より、x軸の正の向きへ進行する電圧波と電流波の比、x軸の負の向きへ進行する電圧波と電流波の比は、場所・時間によらずつねにZ0となることがわかります。これは、電圧の進行波にはつねに同方向に伝搬する電流の進行波が伴うことを意味します(両者は同相となります)。Z0を特性インピーダンスといいます。
特性インピーダンスの概念は、図5のように電圧=水位、電流=水の流れと考えて、進行する波をイメージすると分かりやすいです。電圧波が進行すると、電圧波と同じ位置に電圧波の進行方向と同じ向きの電流が生じ、それらの比が特性インピーダンスZ0です。