ゲインと位相の関係(ボードの定理)
RC回路の周波数特性の考え方 では、1次RC回路の周波数特性を直観的に理解する方法について記述しました。そして、「ゲインの傾きと位相は関係している」と締めくくりました。このページでは、ゲインと位相の関係を定式化した「ボードの定理」について考えます。
ボードの定理とは、複素平面の右半面に極がない系(最小位相推移系)のゲインと位相の関係を定式化したもので、簡単に言うと「ゲインの傾きから位相がわかる」と言っています。
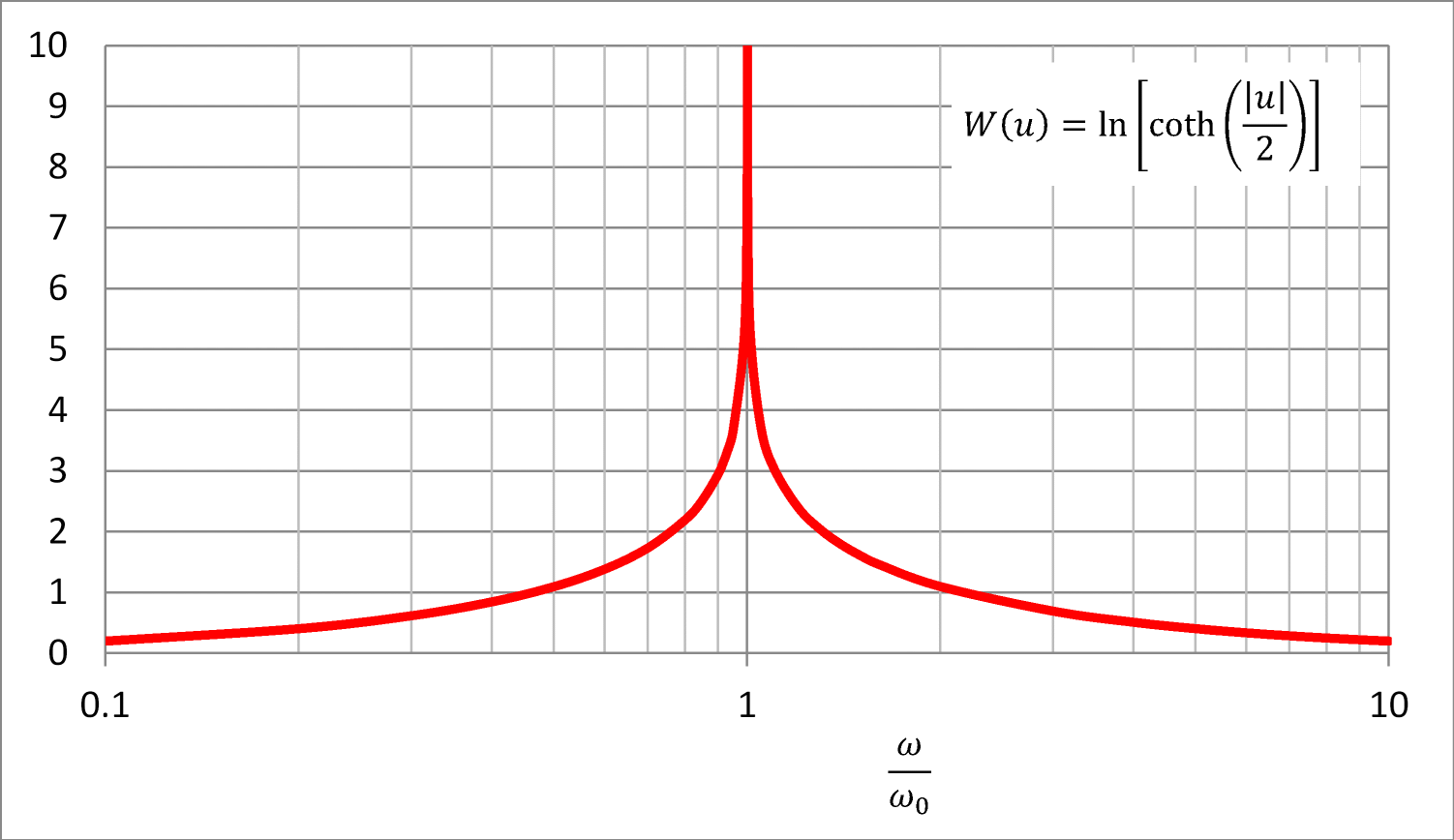
ボードの定理を覚えれば、オペアンプ回路などの位相補償を考える際、ゲインの傾きだけから位相余裕の大・小を判断できるので、非常に有用です。たとえば、開ループゲインが図1(a)と図1(b)の系を比較すると、(a)のほうが(b)よりも0dBとなる周波数ω0における傾きが大きいので位相余裕が小さい(発振しそう)だと分かります。
ボードの定理の証明
複素平面の右半面に極がない系の伝達関数をH(s)とします。角周波数ω0の正弦波に対する伝達関数はH(jω0)ですが、自然対数をとり実部と虚部に分けて表すと
\begin{align} \ln H(j\omega_0)= \ln|H(j\omega_0)|+j\arg H(j\omega_0) \end{align}となります。ln|H(jω0)|がゲイン、arg H(jω0)が位相で、両者の関係を求めるのが目的です。 そのためには、コーシーの積分公式を利用して s=jω0の近傍でlnH(s)を展開します。
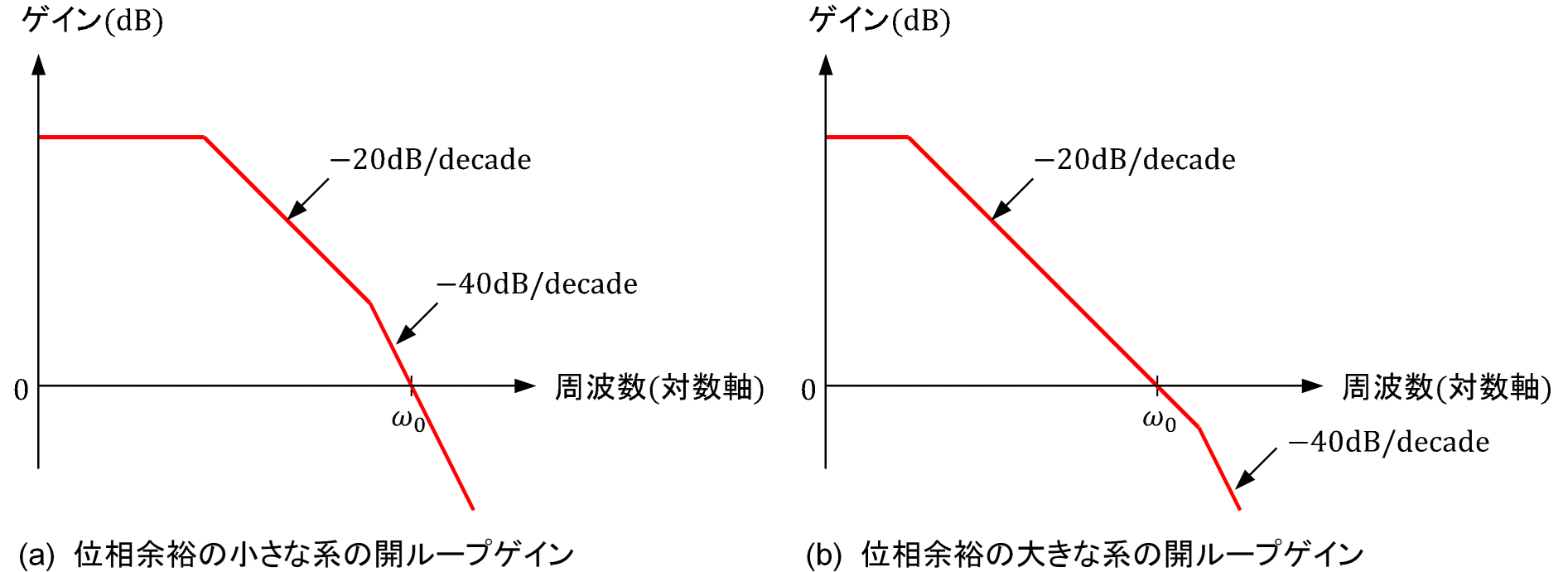
$f_1(s)=\frac{\ln H(s)}{(s+j\omega_0)}$ とおくと、f1(s)はs=jω0の近傍で正則だから、コーシーの積分公式より
\begin{align} &f_1(j\omega_0)=\frac{1}{2\pi j}\int_{C_1}\frac{f_1(s)}{s-j\omega_0}ds\\ \label{eq:bode_2} \rightleftharpoons\ &\ln H(j\omega_0) =\frac{\omega_0}{\pi}\int_{C_1}\frac{\ln H(s)}{(s+j\omega_0)(s-j\omega_0)}ds \end{align}と、lnH(jω0)はs=jω0を中心とした周回積分として表されます(図2)。
一方、$f_2(s)=\frac{\ln H(s)}{(s-j\omega_0)}$ とおいて、f2(s)をs=−jω0を中心とした周回積分で表すと
\begin{align} \label{eq:bode_3} \ln H(-j\omega_0) =-\frac{\omega_0}{\pi}\int_{C_2}\frac{\ln H(s)}{(s+j\omega_0)(s-j\omega_0)}ds \end{align}となります。
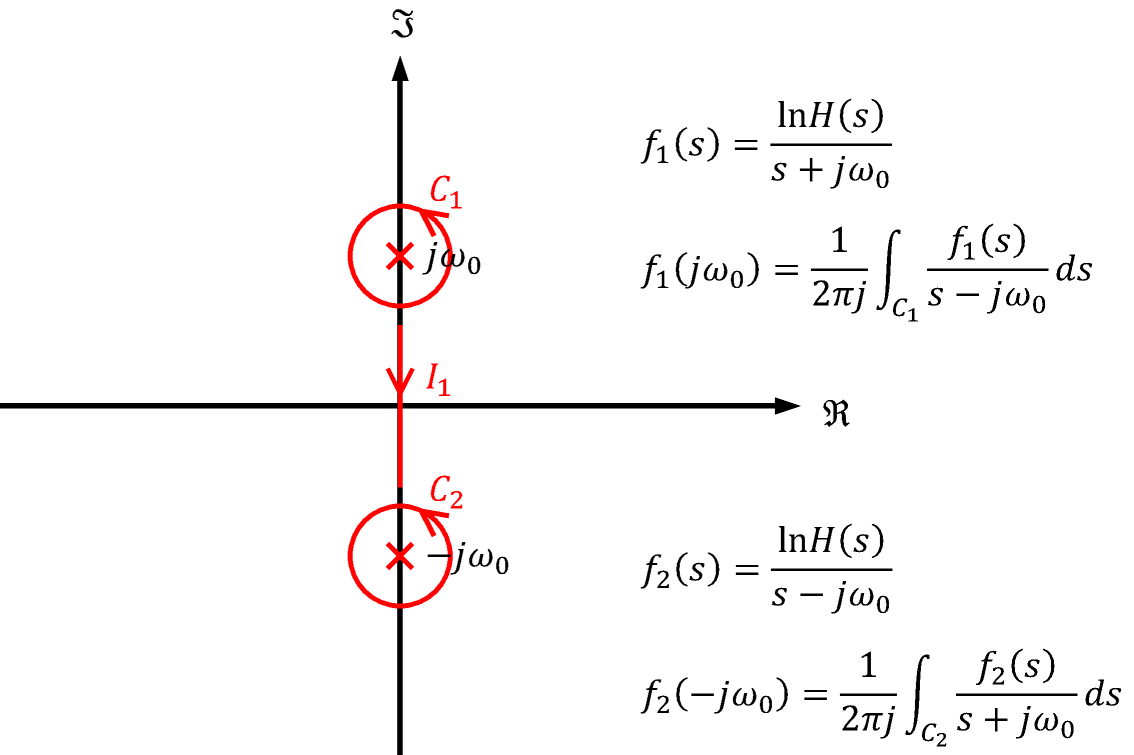
フーリエ変換の性質より、H(−jω0)はH(jω0)の複素共役なので
\begin{align} \ln H(-j\omega_0)=\ln|H(j\omega_0)|-j\arg H(j\omega_0) \end{align}となることに注意して(\ref{eq:bode_2})式と(\ref{eq:bode_3})式の差を求めると
\begin{align} \arg H(j\omega_0)&=\frac{\omega_0}{2\pi j}\left(\int_{C_1}f(s)ds+\int_{C_2}f(s)ds\right)\\ f(s)&=\frac{\ln H(s)}{(s+j\omega_0)(s-j\omega_0)} \end{align}と、位相arg H(jω0)が周回積分C1とC2の和として表されます。さらに、留数定理を利用して図3のように積分路を変更すると
arg H(jω0)の展開式
となります(H(s)は右半面に極をもたないのでこのような変形が可能です)。この式を計算するとゲインと位相の関係が求まります。
$\phi(\omega)=\arg H(j\omega)$, $A(\omega)=\ln|H(j\omega)|$と表記し、(\ref{eq:bode_4})式を計算すると次式が得られます。
ボードの定理
さらに、u=ln(ω/ω0)とおいて周波数も対数軸とし、双曲線関数を使用して表記すると
ボードの定理(双曲線関数表記)
となります。
ボードの定理の意味
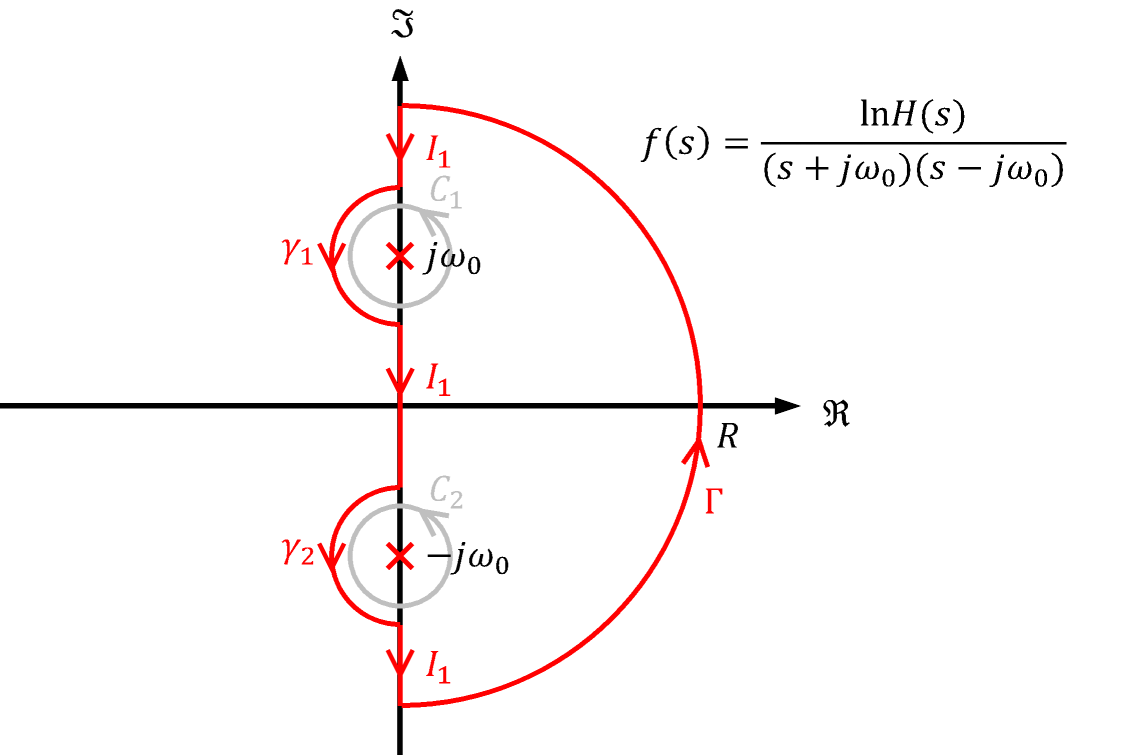
(\ref{eq:bode_5})式は、「角周波数ω0における位相φ(ω0)は、ゲインの傾き$dA/du$に重み関数W(u)を乗じて、全周波数について加え合わせたもの」という意味です。ただし、重み関数W(u)は図4のように周波数ω0 (u=0)で∞、ω0から離れると急速に減衰する関数なので、角周波数ω0における位相は、ω0とその近傍の周波数におけるゲインの傾きでほぼ決まります。
たとえば、ω0及びその近傍におけるゲインの傾きが−20dB/decadeの場合、dA/du=−1 (Aは自然対数としていることに注意: A=ln|H(jω)|)なので
−20dB/decadeの領域の位相
となります。同様に、−40dB/decadeの領域では、dA/du=−2なのでφ≈−πとなります。ただし、
\begin{align} \int_{-\infty}^{\infty}W(u)du=\frac{\pi^2}{2} \end{align}を利用しています。