RC回路の周波数特性の考え方

1次RC回路の周波数特性は、単に式を導出しておわりではなく、キャパシタに電荷が充放電される様子をイメージして理解することが重要です。RC回路の周波数特性を注意深く考えることで、ボードの定理(ゲインと位相の関係)が理解でき、オペアンプ回路の位相補償を考えるとき等に役立ちます。

本来、周波数特性は正弦波を入力したときの応答(出力の振幅・位相がどうなるか)ですが、ここではキャパシタに電荷が充放電される様子を理解しやすくするために、図1のように方形波を印加したときの出力の振幅、位相(位置のずれ)について考えます。

入力信号の周波数が低い場合

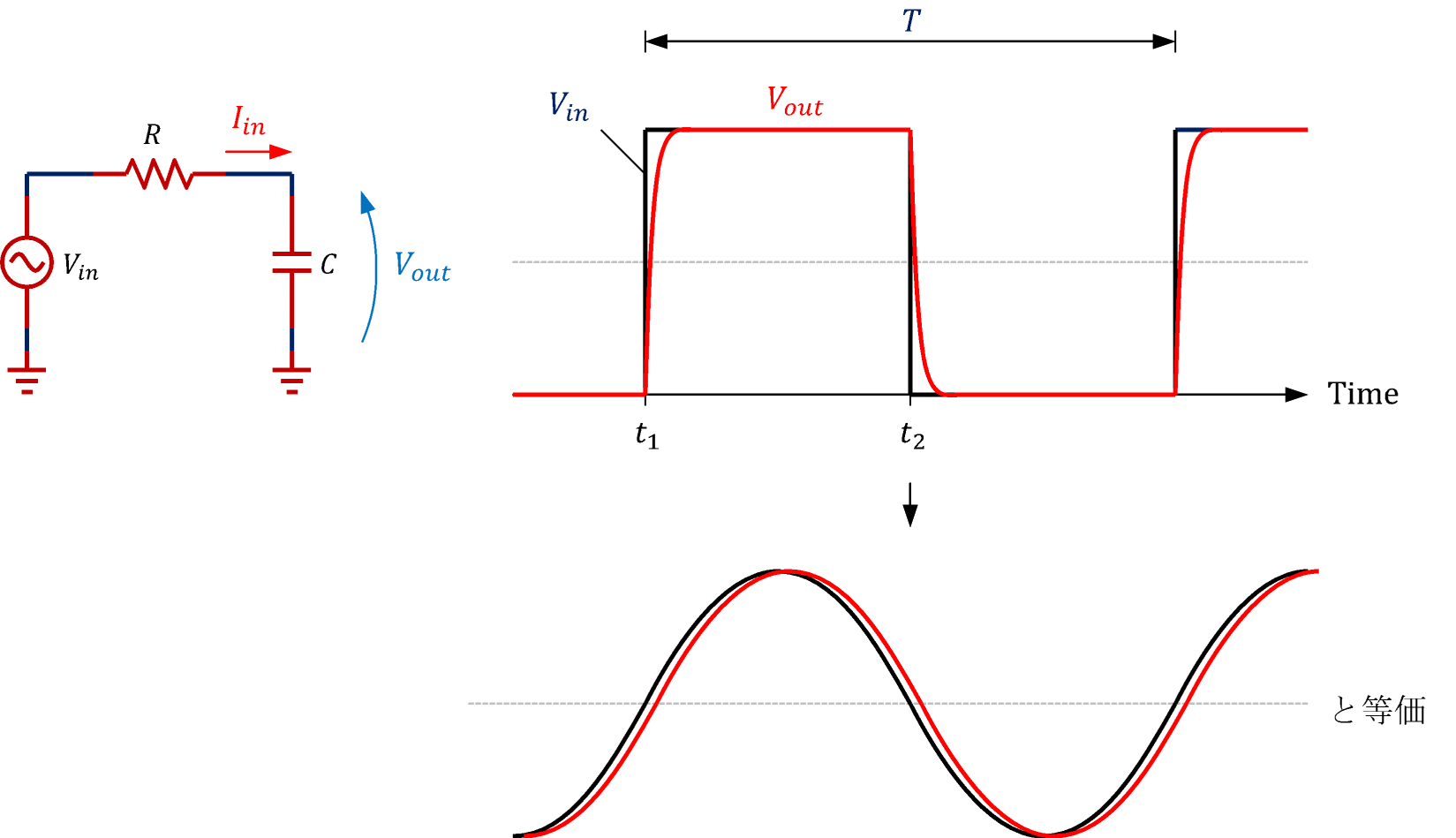
入力信号Vinの周波数が低い場合の応答は図1のようになります。時刻t1でVinがステップ状に立ち上がると、抵抗Rの両端にVinとVoutの差の電圧が印加されるので電流Iin=(Vin−Vout)/Rが流れ、この電流Iinによって運ばれる電荷がキャパシタCに蓄えられることでVoutが上昇します。よって、VoutはVinに対してやや遅れた波形となります。時刻t2でVinが立ち下がった場合も同様に、VoutはVinに対してやや遅れた波形となります。

入力信号の周波数が低い場合は、Voutの立ち上がり・立ち下がり遷移時間に対して周期T が長いので、入力と出力の振幅は同じ、位相も同じとみなせます。

入力信号の周波数を上げると

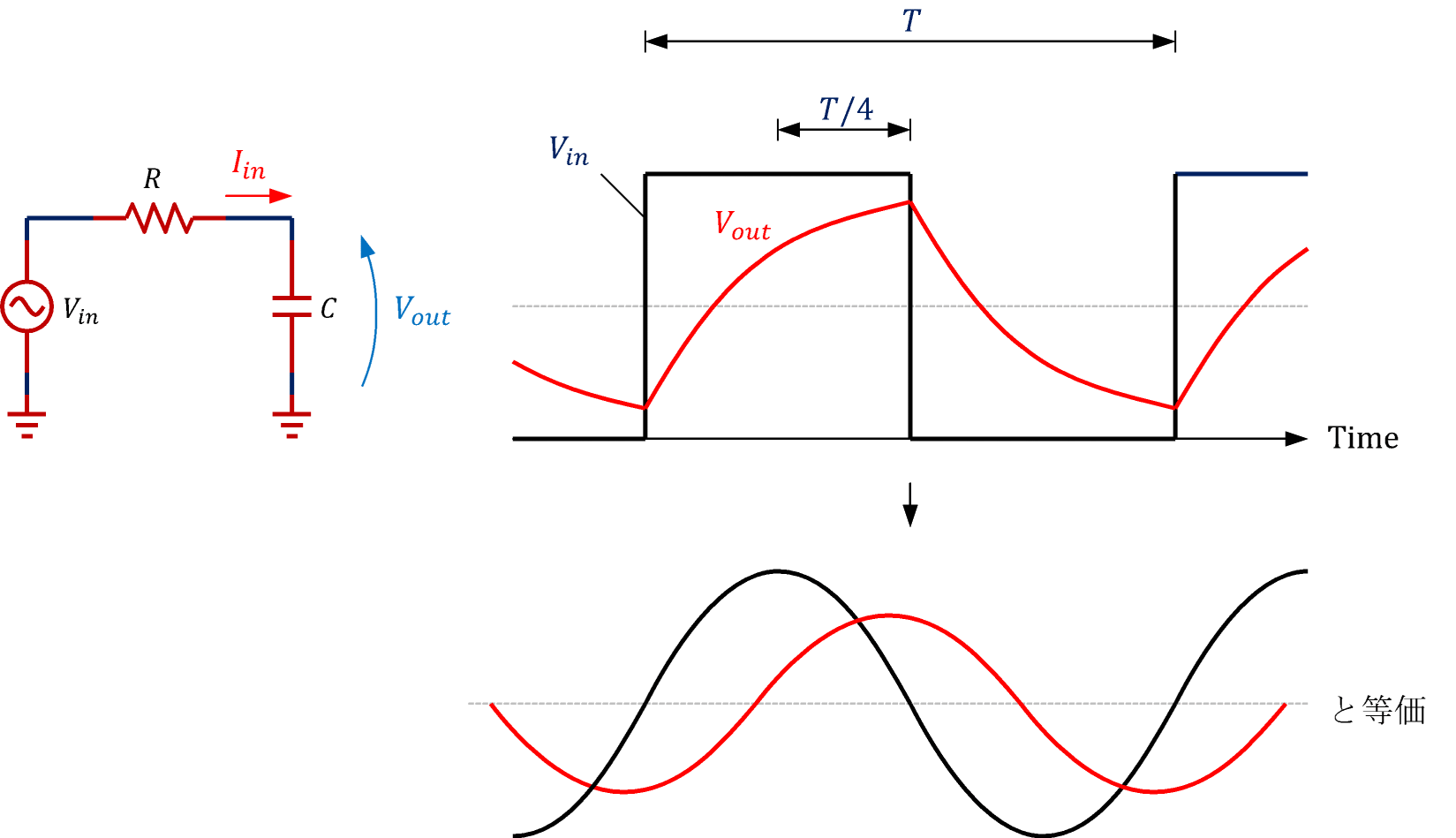
入力信号Vinの周波数を上げると、Voutの立ち上がり時間・立ち下がり時間が無視できなくなります。図2のようにVoutが最終値に達する前にVinの極性が変化するので、VoutはVinに対して振幅が減少した波形となります。

また、Vinのピークの位置に対してVoutのピークの位置は1/4T程度ずれた位置、つまりVinに対してVoutの位相は約π/2だけ遅れた波形となります。

入力信号の周波数をさらに上げると

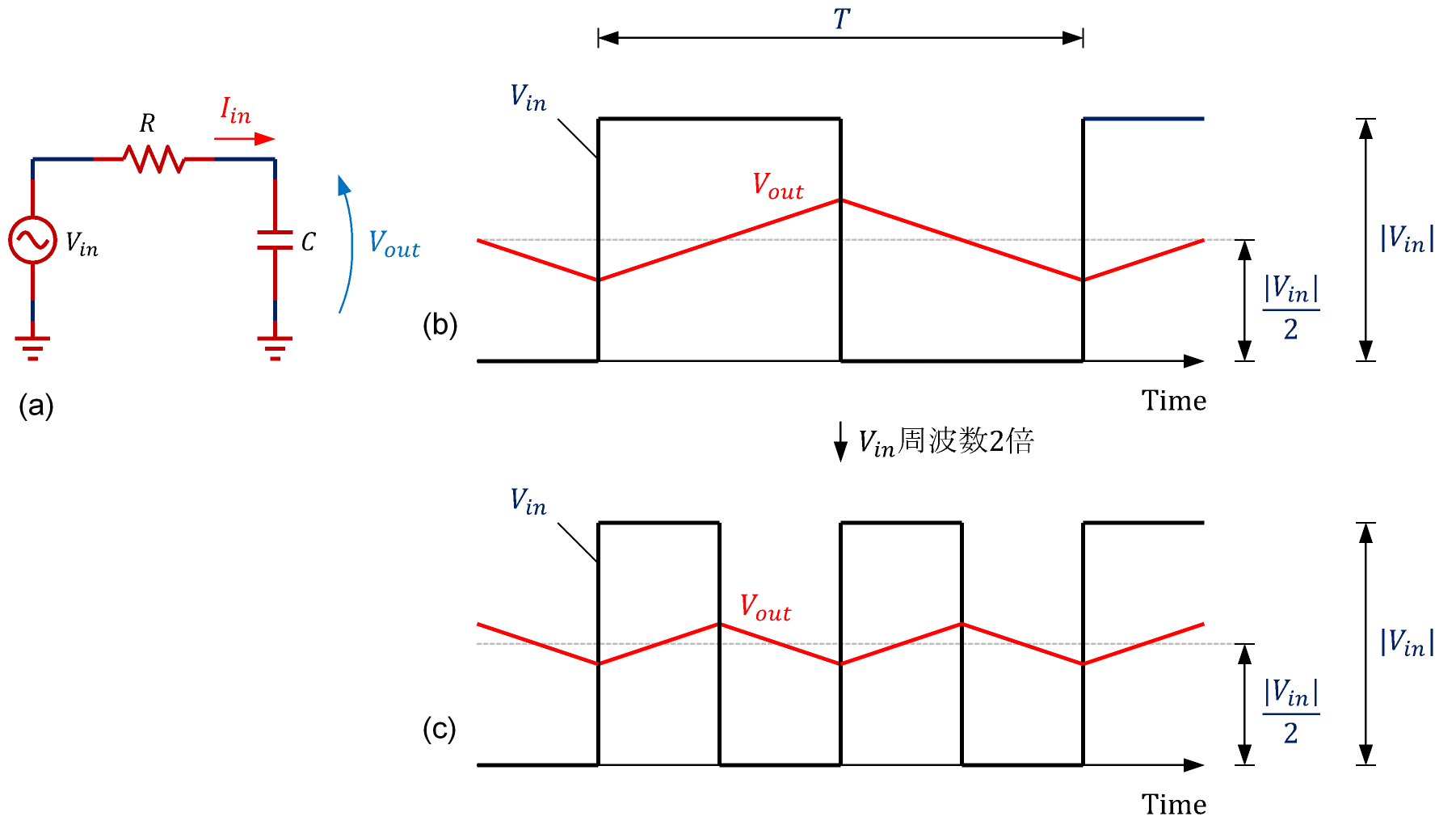
図2よりもさらに入力信号Vinの周波数を上げると、VoutはVinの振幅の1/2の位置(点線の位置)付近でわずかに変化する波形となります。Cを充放電する電流は Iin≈|Vin|/2R とみなすことができ、図3(b)のようにVoutはほぼ直線的に変化します。

ここで、図3(c)のようにVinの周波数を2倍にすると、Voutは(b)の場合と同じ傾きで変化するので、振幅は1/2となります。一方、Vinに対するVoutの位相の遅れは、図3(b),(c)ともπ/2となります。

まとめ

1次RC回路のふるまいをまとめると、以下のようになります。

1次RC回路の周波数特性まとめ

これは、次式のように伝達関数から導出される結果と一致します。

\begin{align} \text{伝達関数:}\quad A(\omega)=\frac{1}{1+j\frac{\omega}{\omega_0}}\ ,\ \omega_0=\frac{1}{RC} \end{align} \begin{align} \text{$\omega\ll \omega_0$の場合:}\quad &A(\omega)\approx 1\ ,\ |A(\omega)|\approx 1\ ,\ \arg[A(\omega)]\approx 0\\ \text{$\omega\gg \omega_0$の場合:}\quad &A(\omega)\approx \frac{1}{j\frac{\omega}{\omega_0}}\ ,\ |A(\omega)|\approx \frac{\omega_0}{\omega}\ ,\ \arg[A(\omega)]\approx -\frac{\pi}{2}\\ \end{align}

周波数特性を描くと図4のようになります。

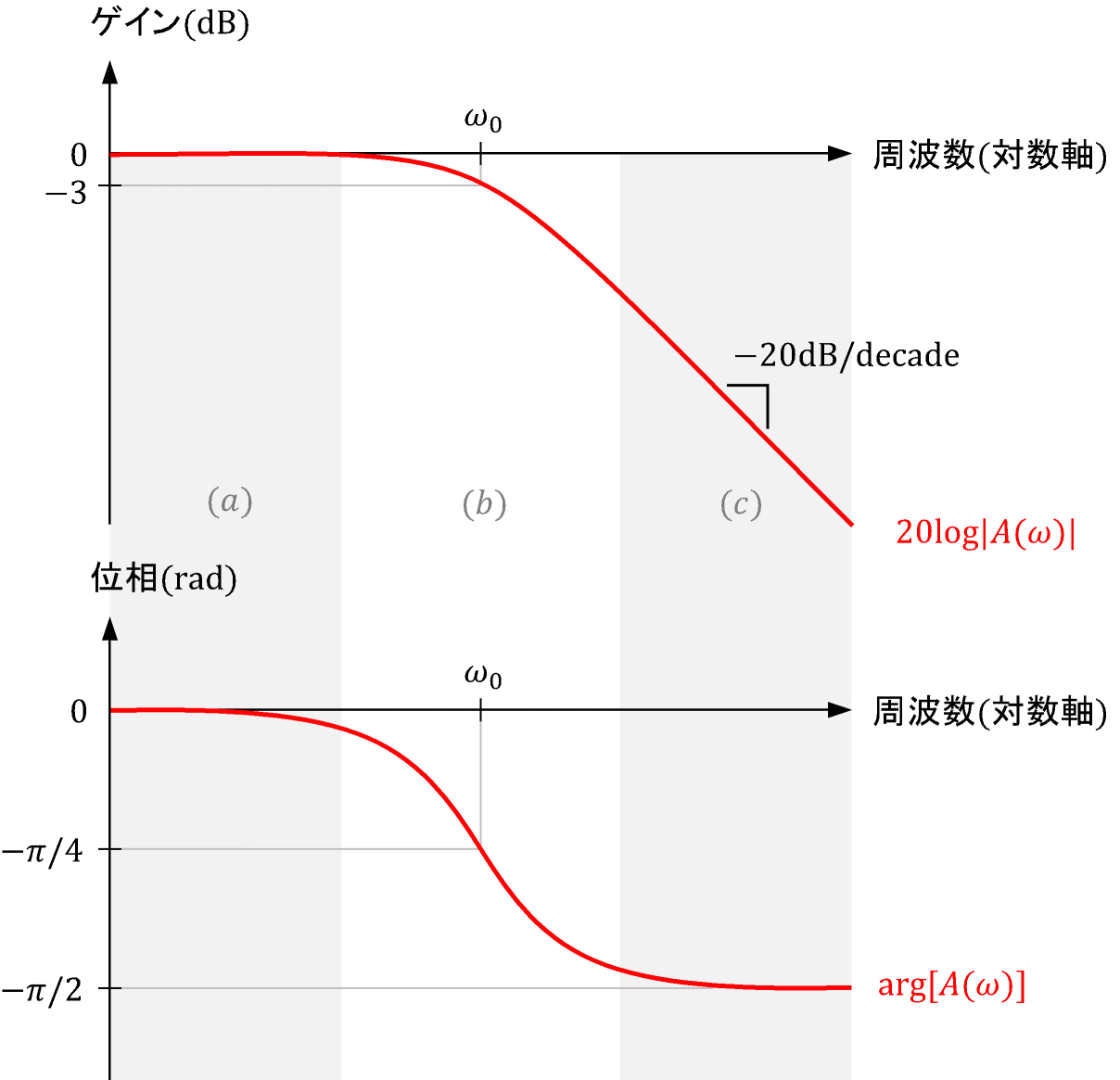
※ ゲインが低下する領域の傾きは、周波数が2倍になる(1オクターブ変化する)と1/2倍となる(6dB低下する)ことから「−6dB/octave」、または周波数が10倍になる(1 decade変化する)と1/10倍となる(20dB低下する)ことから「−20dB/decade」と表記します。

これまでの解説及び図4より、ゲインと位相遅れは互いに関係していることがわかります。この関係を「ボードの定理」といいます。

ボードの定理(ゲインと位相の関係)

となります。(b)の領域のゲインの傾きは、(a),(c)の領域の中間的な値となるので、位相遅れも中間的な値となります。ボードの定理が頭の中に入っていると、位相特性を見なくてもゲインの傾きから位相特性を推測することができるので、位相補償を考えるとき等に役立ちます。