Sパラメータ計算例

通常、Sパラメータは専用のシミュレータを使用して計算しますが、簡単な回路ならば手計算で求めるができます。

Sパラメータの定義と計算方法

Sパラメータは、端子電圧・電流の組(V1,I1),(V2,I2)から得られる入射波成分と反射波成分の組(a1,b1),(a2,b2)を使用して二端子対回路を定式化したものです。詳しくは Sパラメータとはなにかをご参照ください。

Sパラメータの定義

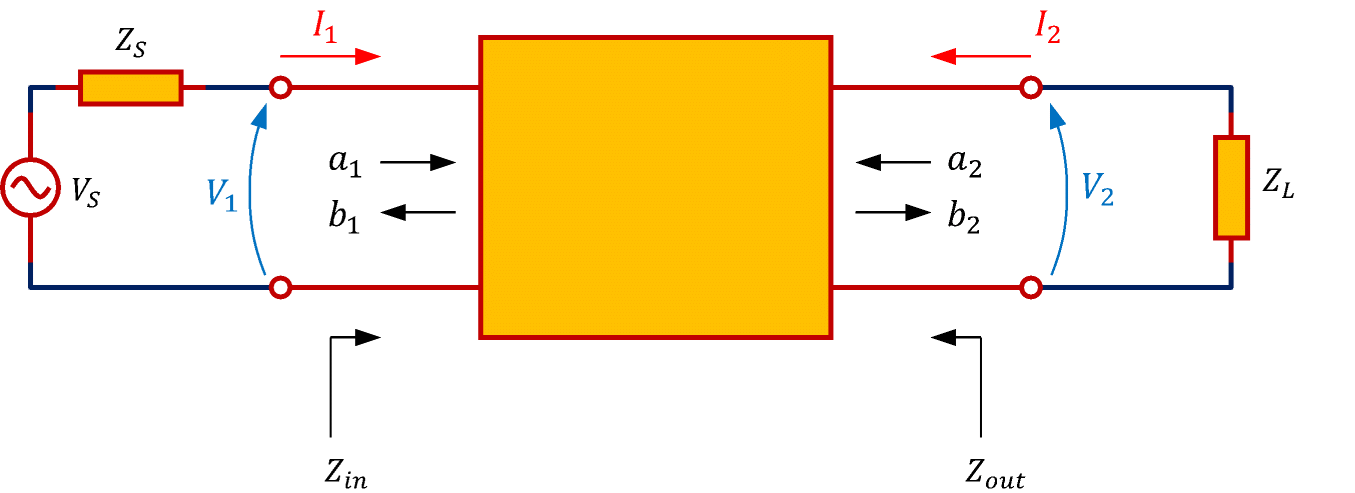
\begin{align} \begin{cases} b_1=S_{11}a_1+S_{12}a_2\\ b_2=S_{21}a_1+S_{22}a_2 \end{cases} \quad \text{ 行列表記: } \begin{bmatrix}b_1\\b_2\end{bmatrix} =\begin{bmatrix}S_{11}&S_{12}\\S_{21}&S_{22}\end{bmatrix} \begin{bmatrix}a_1\\a_2\end{bmatrix} \end{align}

(V1,I1)の組から(a1,b1)、(V2,I2)の組から(a2,b2)を求めるには次式を利用します。Z0は特性インピーダンスですが(またはリファレンスインピーダンスともいいます)、図1のように伝送線路を使用しない回路においては物理的な意味を持たず、電圧・電流の計算結果はZ0の選び方に依存しませんが、通常Z0=50Ωとします。

正規入射波・反射波と端子電圧・電流の関係

\begin{align} \begin{cases} a_1=\frac{1}{2\sqrt{Z_0}}(V_1+Z_0I_1)\\ b_1=\frac{1}{2\sqrt{Z_0}}(V_1-Z_0I_1) \end{cases} \quad\text{ 行列表記: } \begin{bmatrix}a_1\\b_1\end{bmatrix} =\frac{1}{2\sqrt{Z_0}}\begin{bmatrix}1&Z_0\\1&-Z_0\end{bmatrix} \begin{bmatrix}V_1\\I_1\end{bmatrix} \end{align} \begin{align} \begin{cases} a_2=\frac{1}{2\sqrt{Z_0}}(V_2+Z_0I_2)\\ b_2=\frac{1}{2\sqrt{Z_0}}(V_2-Z_0I_2) \end{cases} \quad\text{ 行列表記: } \begin{bmatrix}a_2\\b_2\end{bmatrix} =\frac{1}{2\sqrt{Z_0}}\begin{bmatrix}1&Z_0\\1&-Z_0\end{bmatrix} \begin{bmatrix}V_2\\I_2\end{bmatrix} \end{align}

図1で負荷ZL=Z0とすると、$V_2=-Z_0I_2$となりますが、これを上のa2の式に代入すると、a2=0となることが分かります。同様に、信号源VS=0として信号源インピーダンスZS=Z0とすると、a1=0となることが分かります。このように、回路を特性インピーダンスで終端すると反射波が生じなくなります。

Sパラメータの定義式及び上のa1,b1,a2,b2の式より、各パラメータは次式のようになります。

\begin{align} S_{11} &= \left.\frac{b_1}{a_1}\right|_{a_2=0}=\left.\frac{V_1-Z_0I_1}{V_1+Z_0I_1}\right|_{Z_L=Z_0} =\left.\frac{Z_{in}-Z_0}{Z_{in}+Z_0}\right|_{Z_L=Z_0}\\ S_{21}&= \left.\frac{b_2}{a_1}\right|_{a_2=0} =\left.\frac{V_2-Z_0I_2}{V_1+Z_0I_1}\right|_{Z_L=Z_0} =\left.\frac{2V_2}{V_S}\right|_{Z_L=Z_0,Z_S=Z_0} =\left.\frac{V_2}{V_S/2}\right|_{Z_L=Z_0,Z_S=Z_0} \end{align}

Zinは、図1の回路をZ0で終端したときの入力インピーダンスです。 S21の式の分母の$V_1+Z_0I_1$は、信号源インピーダンスを$Z_S=Z_0$とすると$V_S$となります。

S12,S22は左右を逆にして同様に求めます。

Sパラメータ計算例: シリーズ抵抗

図2(a)の回路について、特性インピーダンスZ0=50ΩとしてSパラメータを計算します。

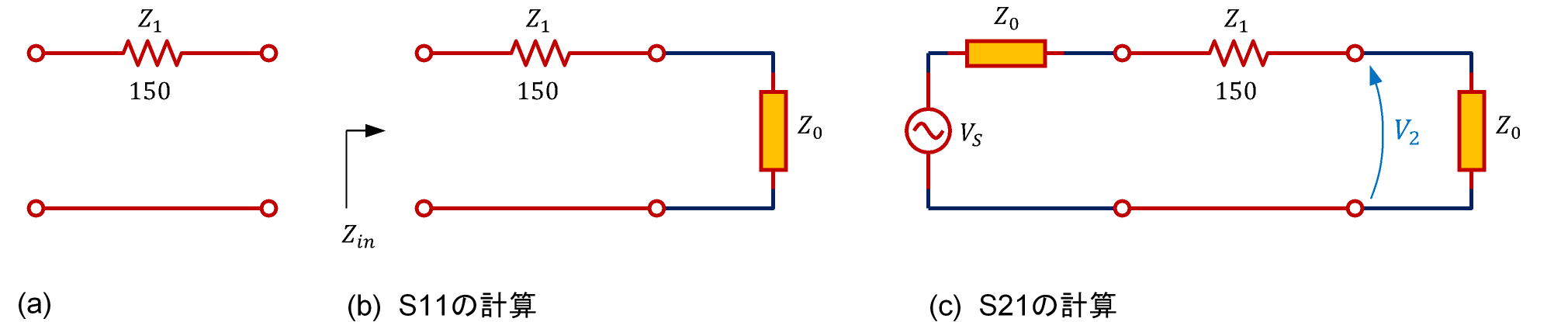
S11の計算: 図2(b)

\begin{align} Z_{in}&=Z_1+Z_0=200\\ S_{11}&=\frac{Z_{in}-Z_0}{Z_{in}+Z_0}=\frac{150}{250}=0.6 \end{align}

S21の計算: 図2(c)

\begin{align} V_2&=\frac{Z_0}{Z_0+Z_1+Z_0}=\frac{50}{250}V_S=0.2V_S\\ S_{21}&= \frac{V_2}{V_S/2}=0.4 \end{align}

回路は左右対称なので、S12=S21, S22=S11となります。よって、Sパラメータは

\begin{align} S=\begin{bmatrix}0.6&0.4\\0.4&0.6\end{bmatrix} \end{align}

となります。