回路シミュレータの基礎: 用語・原理
回路シミュレータを使いこなすためには、シミュレータの原理に関するある程度の知識も必要となります。このページでは基本用語と原理について解説しています。
基礎事項
回路シミュレータのアルゴリズムは、1970年代にカリフォルニア大学バークレー校で開発されたシミュレータ「SPICE」(スパイス)を基本としています。商用・非商用を問わず、アナログ回路シミュレータの多くはSPICEを改良したもので、一般に「SPICE系シミュレータ」とよばれています。 以降、SPICE系シミュレータを単に「回路シミュレータ」とよびます。
図1のように、回路シミュレータは、回路の接続情報・回路定数・シミュレーションコマンドを記述したファイル(ネットリスト)を読み、ネットリストに記述された回路の接続情報・回路定数から回路方程式を自動的につくり、解きます。通常、ネットリストは回路図エディッタが自動的に生成します(テキストエディッタを使用して書くこともできます)。
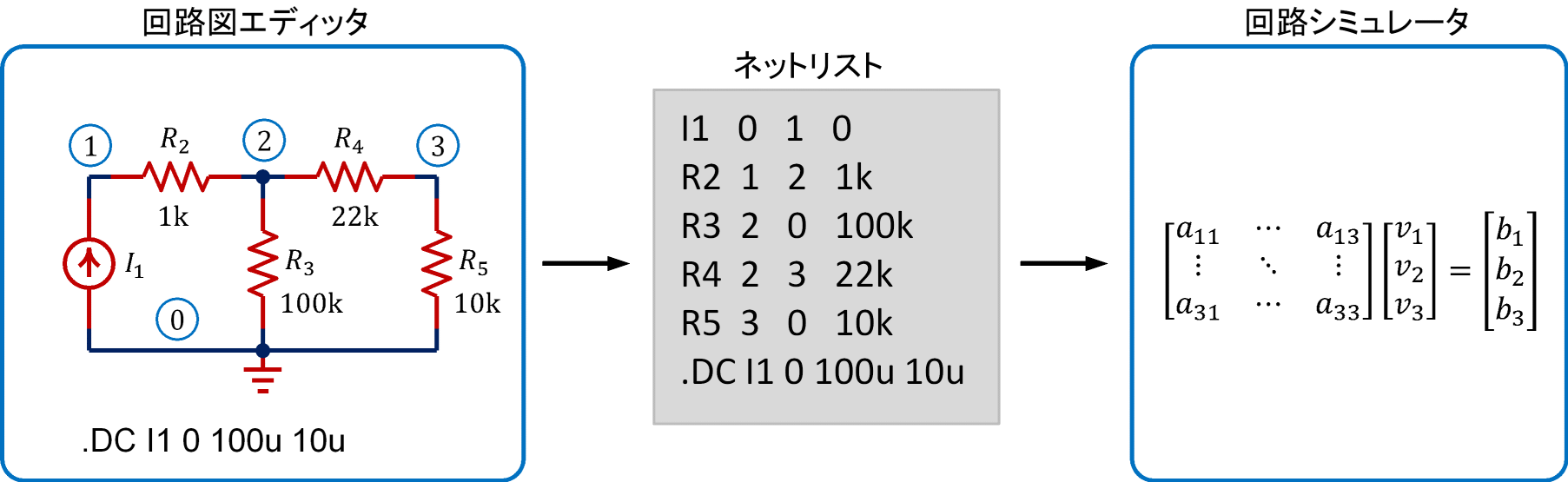
ネットリストの書式
エレメントステートメント(回路素子記述文)
図1のネットリストの上から5行目までのように、回路素子名・接続ノード名・素子値を空白区切りで記述した文です。回路素子名の接頭辞(1文字目)は抵抗の場合は「R」、容量の場合は「C」のようにあらかじめ定義されています。たとえば、ノード「1」と「2」の間に1kΩの抵抗が接続されている場合は「R2 1 2 1K」となります(図1のネットリスト参照)。大文字・小文字は区別されませんが、通常大文字で記述します。
シミュレーションコマンド(ドットコマンド)
図1のネットリストの最終行のように、解析の種類(DC解析、AC解析など)、計算条件(計算精度、解析温度など)、ダイオードやトランジスタのモデルをシミュレータに指示する文で、ドット「.」で始まることから「ドットコマンド」とよばれます。たとえば、電流源I1の電流を0から100uAまで10uAステップで変化させてシミュレーションする場合は「.DC I1 0 100u 10u」、電圧源V1の電圧を0Vから5Vまで0.1Vステップで変化させる場合は「.DC V1 0 5 0.1」と記述します。
スケーリング記号(MEG, K, M, U)
1kΩ抵抗は「1000」,「1E3」,「1K」のように記述することができます。スケーリング記号「K」はキロ(×1000)という意味です。スケーリング記号の定義は表1のようになっています。
※「M」は「メガ」ではなく「ミリ」と解釈されることに注意してください。
| スケーリング記号 | 読み | 意味 |
|---|---|---|
| P | ピコ | ×10-12 |
| N | ナノ | ×10-9 |
| U | マイクロ | ×10-6 |
| M | ミリ | ×10-3 |
| K | キロ | ×103 |
| MEG | メガ | ×106 |
| G | ギガ | ×109 |
グラウンドのノード名は「0」、必ず使用すること
図1の回路方程式は
\begin{align} \begin{bmatrix} \frac{1}{R_2}&-\frac{1}{R_2}&0\\ -\frac{1}{R_2}&\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}&-\frac{1}{R_4}\\ 0&-\frac{1}{R_4}&\frac{1}{R_4}+\frac{1}{R_5}\\ \end{bmatrix} \begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix} =\begin{bmatrix}I_1\\0\\0\end{bmatrix} \end{align}と未知数がv1,v2,v3、方程式の本数が3本となります。未知数の数と方程式の本数が同じなので、この方程式は解くことができ、グラウンド(ノード0)を基準とした電圧としてv1,v2,v3が得られます。
グラウンド(ノード0)は必ず使用しなければなりません。仮にグラウンド を置き忘れると、電圧の基準となるノードがない上、未知数の数と独立な方程式の本数が一致せず、解くことができなくなります。
DC解析概要: ニュートン法による動作点解析
DC解析とは、図2のように電圧源または電流源の値をスイープして、それぞれのスイープ値における回路の動作点を計算する解析です。DC解析時はキャパシタはオープン(開放)、インダクタはショート(短絡)として扱われます。
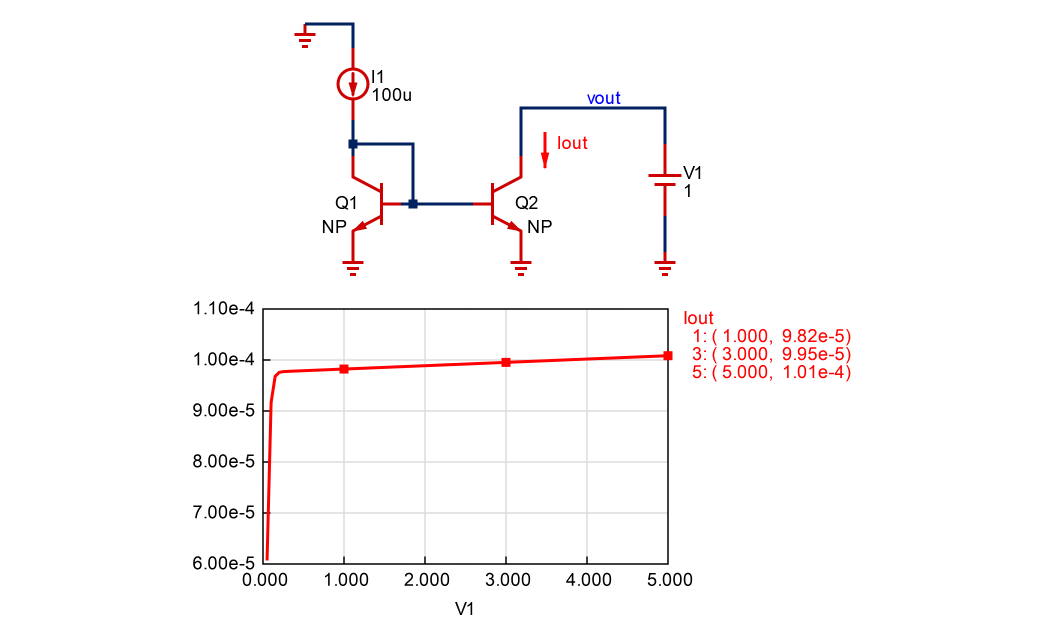
ダイオードやトランジスタのように電流-電圧特性が非線形な素子が含まれる場合は、非線形素子の電流-電圧特性を線形近似して回路方程式をつくり、解きます。そして、得られた解を動作点として再び線形近似して回路方程式を解きます。この作業を繰り返して、解がある一定範囲内に収束したら解析を終了し、この収束値を解とします。このようにして非線形方程式を解く方法をニュートン法といいます。
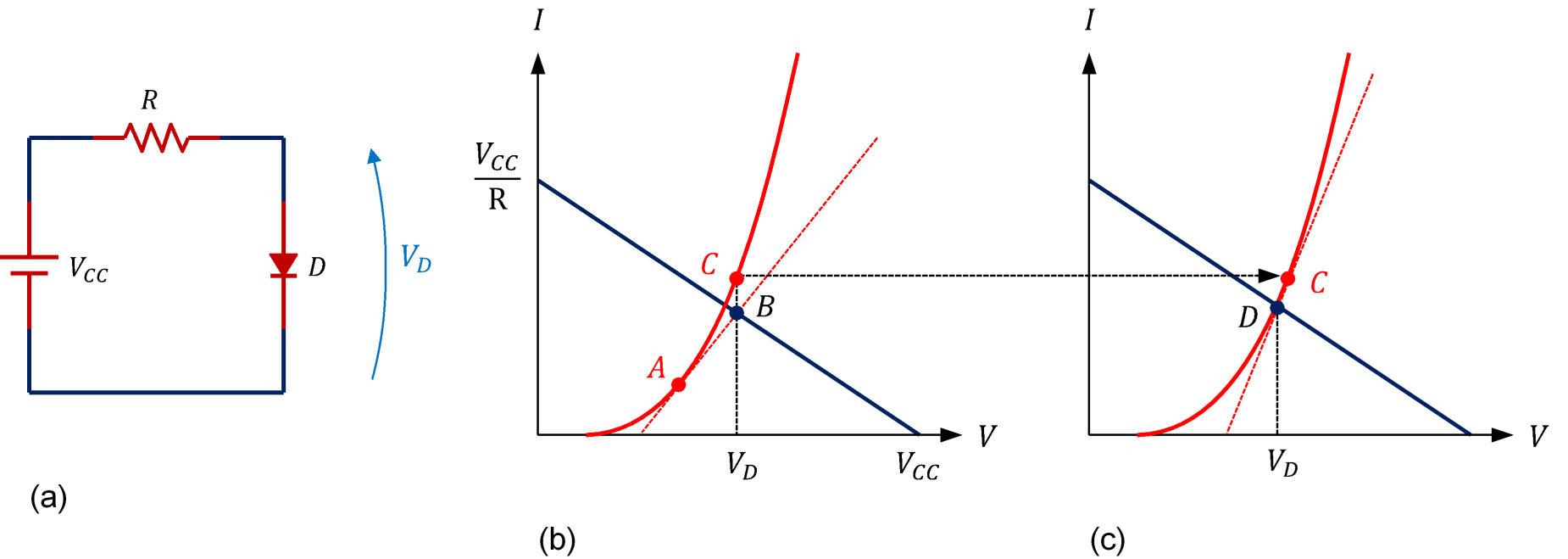
図3(b)はダイオード回路の負荷線を図示したもので、A点でダイオード特性を点線のように線形近似すると解(B点)が得られます。次に、ダイオードの印加電圧がB点と同じとなる点(C点)でダイオード特性を線形近似すると解(D点)が得られます。このように、非線形方程式の解は、線形方程式を繰り返し解くことによって得られます。
シミュレーションの相対誤差は0.1%、電圧分解能は1uV、電流分解能は1pA
一般にシミュレーションの確度(正確さ)は使用するモデルの確度に依存しますが、「たとえ正確なモデルを使用しても、回路シミュレータの計算結果は厳密ではない」ということを認識しておく必要があります。
ニュートン法は、回路を線形化して解く作業を繰り返しおこない、解が一定範囲内に収束したら解析を終了しますが、収束判定は、デフォルト設定(標準設定)で「相対誤差 0.1%(有効数字4桁)、電圧分解能 1uV、電流分解能 1pA」となっています(表2)。これらのパラメータは、.OPTIONSコマンドで変更することもできます。
| パラメータ | 意味 | デフォルト値 |
|---|---|---|
| RELTOL | 相対誤差 | 0.001 |
| VNTOL | 電圧分解能 | 1u |
| ABSTOL | 電流分解能 | 1p |
相対誤差が0.1%ですから、たとえばノード電圧の真値が1Vの場合、シミュレーション結果は最大で1mV程度の誤差が含まれます。また、電圧分解能 が1uVですから、たとえばシミュレーションによってノード電圧10.23uVが得られた場合、小数点以下の数値は信頼できません。
回路シミュレータは回路解析に特化したシミュレータ
電子回路を試作して電圧や消費電流を測定して動作チェックをする際、一般に、電圧1mVの測定誤差は無視しても差し支えありませんが、電流1mAの測定誤差は無視できません。このように、電圧と電流は次元が異なり、要求される分解能も異なります。
回路シミュレータは、表2のように電圧と電流の収束判定値を別々に設定した「回路解析に特化したシミュレータ」で、汎用の数値解析ソフトではありません。 機械系やデバイス系のような電圧・電流とは異なる次元をもつ物理量のシミュレーションに回路シミュレータを利用することも可能ですが、収束判定の設定を適切におこなわないと、信頼のできる結果が得られません。
また、汎用数値計算ソフトを回路シミュレータとして利用するのも困難だと思われます。なぜなら、電圧に対する収束判定と電流に対する収束判定を別々に設定するのが困難だからです。 さらに、回路シミュレータでは過渡解析におけるタイムステップ(時間刻み幅)の自動調整機能が必須ですが、汎用数値計算ソフトを使用してこの機能を作り込むのは困難だと思われます。
過渡解析概要: 台形法による数値積分
過渡解析とは、回路にパルスや正弦波を入力したときのノード電圧の時間変化を刻一刻とシミュレーションする解析で、時刻をt0,t1,t2,...と進めながら、各時刻における動作点をDC解析と同じ手順で計算します。ただし、キャパシタ・インダクタの電流-電圧特性(微分方程式)は台形法により差分方程式で近似します。
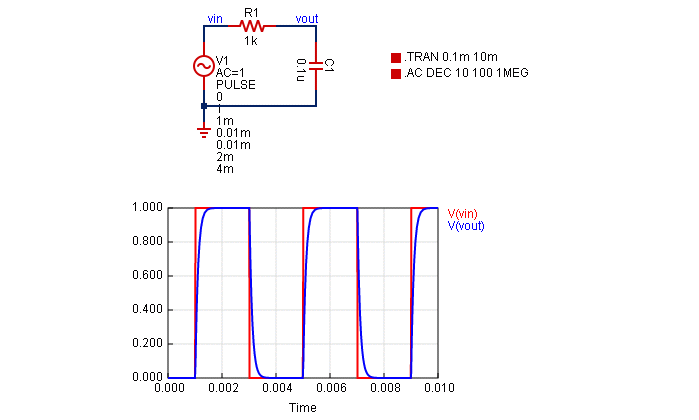
キャパシタの電圧・インダクタの電流の時間積分: 台形法
キャパシタ、インダクタの電流-電圧特性は
\begin{align} \text{微分形表記:}\quad &\frac{dx}{dt}=f(x,t)\\ \text{積分形表記:}\quad &x(t_{n+1})=x(t_n)+\int_{t_n}^{t_n+h_n}f(x(\tau),\tau)d\tau\ , \ t_{n+1}=t_n+h_n \end{align}と表されます。$x$はキャパシタの場合は電圧、インダクタの場合は電流です。hnはタイムステップ(時間の刻み幅)です。積分形表記の右辺第2項の時間積分は、差分方程式で近似します。近似方法の代表的なものに、前進オイラー法、後進オイラー法、台形法(図5)がありますが、多くの回路シミュレータは台形法を採用しています。
\begin{align} \text{台形法:}\quad &x_{n+1}=x_n+\frac{f(x_n,t_n)+f(x_{n+1},t_{n+1})}{2}h_n\\ \text{ただし}\quad &x_n=x(t_n),\ x_{n+1}=x(t_{n+1}),\ h_n=t_{n+1}-t_n \end{align}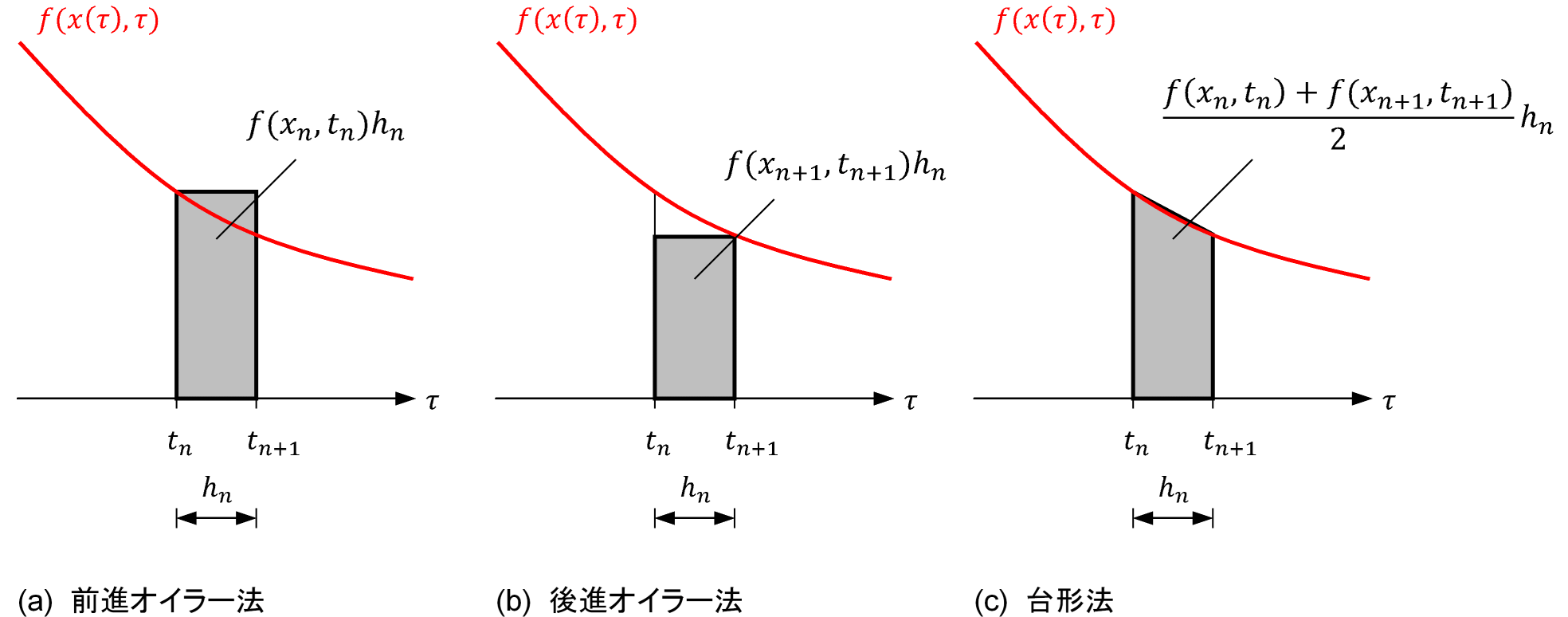
台形法によって生じる数値リンギング
キャパシタ・インダクタを含む回路のシミュレーションにおいて、多くの回路シミュレータは台形法による数値積分を利用していますが、積分のタイムステップ(時間刻み幅)が大きいと数値リンギング(数値的な振動波形)が生じます。 図6は1次RC回路の単位ステップ応答について、タイムステップを等間隔としてシミュレーションした結果ですが、タイムステップを小さくした場合(図6(a))は理論どおりの指数関数特性となりますが、タイムステップが大きい場合(図6(b))は数値リンギングが生じています。
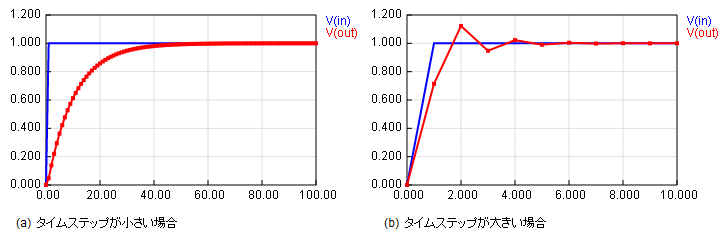
通常、回路の中には時定数が大きい部分・小さい部分が混在しているので、仮に等間隔のタイムステップでシミュレーションを実行すると、信号が急しゅんに変化する位置で数値リンギングが生じるので信頼できる結果が得られません。
数値リンギングを抑えるために、回路シミュレータは信号の変化の度合いに応じてタイムステップを自動的に調整する機能を備えています。 よって、スイッチング回路、発振回路など、頻繁に信号が急しゅんに変化する回路では、シミュレーション時間が長くなります。
タイムステップを自動調整しても、回路形式・回路定数によっては数値リンギングが現れる場合があります。数値リンギングの波形は、図6(b)のように1シンボル点ごとに山・谷・山・谷,...を繰り返す形となるのが特徴です。